티스토리 뷰
#include <stdio.h>
#include <stdlib.h>
long long tree[600000] = {}, start[200001]={}, end[200001]={}, dif[200001] = {}, ETT=0;
char v[200001] = {};
typedef struct list{ //단방향 리스트
struct list * next;
long long val;
}list;
void insert(int x, int y, list vec[]) { //리스트 삽입, x을 기준으로 봅니다.
list * newNode = (list*) malloc(sizeof(list));
newNode->val = y;
newNode->next = vec[x].next;
vec[x].next = newNode;
}
void dfs(int x, int y, list vec[]) { //ETT 및 깊이 구하기
v[x] = 1;
start[x] = ++ETT;
dif[x] = y;
for(list *p = vec[x].next; p!=NULL; p=p->next) if(!v[p->val]) dfs(p->val,y+1,vec); //한번 dfs로 방문한 노드는 더 이상 방문하지 않음
end[x] = ETT;
return;
}
void update(int s, int e, int node, int index) { //단일 갱신
if(s>index || e<index) return;
++tree[node]; //1씩 증가
if(s==e) return;
int m=(s+e)/2;
update(s,m,node*2,index);
update(m+1,e,node*2+1,index);
return;
}
long long find(int s, int e, int node, int l, int r) { //범위 수정
if(s>r || e<l) return 0;
if(l<=s && e<=r) return tree[node];
int m=(s+e)/2;
return find(s,m,node*2,l,r) + find(m+1,e,node*2+1,l,r);
}
int main(void) {
int n, c, m, a, b;
scanf("%d %d",&n,&c);
list* vec = (list*) malloc(sizeof(list)*(n+1));
for(int i=1; i<=n; i++) vec[i].next = NULL;
for(int i=1; i<n; i++) { //간선 입력 받기
scanf("%d %d",&a,&b);
insert(a,b,vec); //어디가 상위노드인지 모르니
insert(b,a,vec); //양쪽으로 삽입
}
dfs(c,1,vec); //주의 : root의 번호는 1이 아니라 c입니다!!!!!
scanf("%d",&m);
while(m--) { //query
scanf("%d %d",&a,&b);
if(a==1) update(1,n,1,start[b]); //update
else printf("%lld\n",find(1,n,1,start[b],end[b])*dif[b]); //find
}
}
풀이 : segment tree, euler track trick
물을 1, 2, 3..... 이렇게 1씩 증가시키면서 물을 주는 것을 구현하기는 힘듭니다. 그대신 segment tree에
특정 그래프의 노드에 물을 몇 번 주었는지를 저장합니다.
그리고 ETT을 활용하여 그래프를 세그먼트 트리에 적용시키게 하면, 특정 그래프의 노드를 root로 한 서브트리의 모든 노드들의 방문 횟수의 합을 구할 수 있게 됩니다. (시작번호 ~ 종료번호)
이 방문 횟수의 합에 특정 그래프의 노드에 물을 뿌릴때의 양을 곱하면 됩니다.
특정 노드에 대한 물의 양은 dfs의 탐색 깊이와 같습니다.
ETT는 dfs로 구현을 하다보니, 자연스레 탐색 깊이를 구하는 코드도 따로 추가해 주면 됩니다.
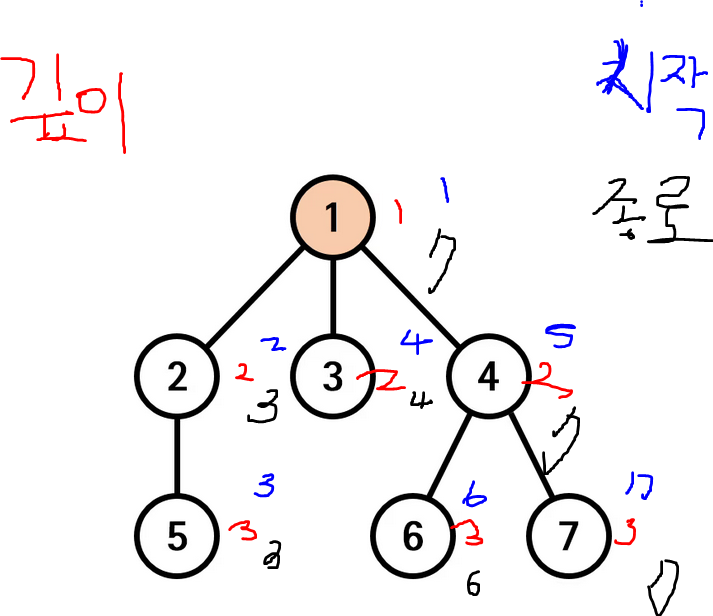
0. segment 을 위한 배열, ETT의 시작번호와 종료번호를 담기위한 배열, dfs시 깊이를 저장하기 위한 배열, 이 그래프의 노드가 dfs에서 다뤄젔는지를 판단하기위한 배열을 미리 만들어 놓습니다.
1. n, c을 입력받습니다.
2. 벡터 역할을 할 단방향 리스트 구조체를 만들고 동적할당을 받습니다.
3. 벡터를 초기화 하고, 그래프의 간선을 입력 받습니다. 간선 정보자체론 어디가 상위노드이고 하위노드인지 알 수 없으니, 양방향 간선이라 생각하고 벡터에 순서만 바꾼채로 저장합니다 (한 간선을 방향 두개로)
4. ETT을 실행합니다. 이때, 시작번호, 종료번호 뿐만이 아니라 깊이도 저장해줍니다. 또한 한번 방문했던 그래프의 노드는 다시 방문하지 않도록 v[]을 활용합니다.
5. query을 m번 실행합니다.
5.1 update는 단일수정이며, 1 증가시킵니다.
5.2 find은 범위 탐색이며, 시작번호 종료번호를 이용하여, 찾고자하는 노드를 서브트리의 root로 여긴 다음, 이 서브트리의 누적합을 구하고 이것을 찾고자 하는 노드의 dif을 곱해줍니다. (그리고 이것을 출력합니다)
'c언어 > BAEKJOON' 카테고리의 다른 글
| c언어 7423번 디스크 트리 (백준) (0) | 2024.09.26 |
|---|---|
| c언어 14725번 개미굴 (백준) (0) | 2024.09.26 |
| c언어 18437번 회사 문화 5 (백준) (0) | 2024.09.06 |
| c언어 14287번 회사 문화 3 (백준) (0) | 2024.09.05 |
| c언어 2820번 자동차 공장 (백준) (0) | 2024.09.04 |
- Total
- Today
- Yesterday
- Segment Tree
- DP
- 백준
- 문자열
- C++
- 기하학
- 스택
- find
- 그리디
- java
- 1835
- XOR
- 브루트포스
- 세그먼트 트리
- PASCAL
- 정렬
- 그래프
- DFS
- 누적 합
- 1835번
- Krustal
- 덱
- union
- BFS
- 누적합
- 최소 스패닝 트리
- Lazy Propagation
- C언어
- 구현
- 오프라인 쿼리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
