티스토리 뷰
#include <stdio.h>
#include <stdlib.h>
int tree[266000]={},lazy[266000]={}; //lazy propagation
int ETT = 0; //오일러 경로 트릭에 사용할 변수
typedef struct list { //리스트를 구성할 노드의 구조체
struct list * prev;
struct list * next;
int val;
} list;
void insert(int sup, int sub, list vec[]) { //리스트 삽입
list *newNode = (list*) malloc(sizeof(list));
newNode->val = sub;
newNode->prev = vec+sup;
newNode->next = vec[sup].next;
if(vec[sup].next != NULL) vec[sup].next->prev = newNode; //아무것도 없는 경우
vec[sup].next = newNode;
}
void dfs(int x, list vec[], int start[], int end[]) { //오일러 경로 트릭
start[x] = ++ ETT;
for(list *p = vec[x].next; p!=NULL; p=p->next) dfs(p->val, vec, start, end);
end[x] = ETT;
}
void lazyU(int s, int e, int node) { //미룬거 수정
if(lazy[node]) {
tree[node] += (e-s+1) * lazy[node];
if(s!=e) {
lazy[node*2] += lazy[node];
lazy[node*2+1] += lazy[node];
} lazy[node] = 0;
} return;
}
void update(int s, int e, int node, int l, int r, int dif) { //갱신
lazyU(s,e,node); //미룬거 수정
if(s>r || e<l) return; //범위 벗어남
else if(l<=s && e<=r) { //범위에 속함
tree[node] += (e-s+1) * dif;
if(s!=e) { //말단 노드가 아니라면
lazy[node*2] += dif;
lazy[node*2+1] += dif;
} return;
}
int m=(s+e)/2; //범위에 걸치면 하위 노드로
update(s,m,node*2,l,r,dif);
update(m+1,e,node*2+1,l,r,dif);
return;
}
int find(int s, int e, int node, int index) { //찾기
lazyU(s,e,node); //미룬거 수정
if(s>index || e < index) return 0; //범위 벗어남
if(s==e) { //단일 범위일 때
if(s==index) return tree[node]; //찾고자 하는 곳이라면
else return 0; //아니라면
}
//위의 경우가 아닌 경우 하위노드로
int m=(s+e)/2;
return find(s,m,node*2,index) + find(m+1,e,node*2+1,index);
}
int main(void) {
int n,m,tmp;
scanf("%d %d",&n,&m); //n, m 입력
//동적 할당
int *start = (int*) malloc(sizeof(int)*(n+1));
int *end = (int*) malloc(sizeof(int)*(n+1));
list *vec = (list*) malloc(sizeof(list)*(n+1));
//입력 받기
for(int i=1; i<=n; i++) {
scanf("%d",&tmp);
if(tmp != -1) insert(tmp, i, vec);
}
dfs(1,vec,start,end); //ETT
while(m--) { //query
int a,b,c;
scanf("%d %d",&a,&b);
if(a==1) {
scanf("%d",&c);
update(1,n,1,start[b],end[b],c); //갱신
}
else {
printf("%d\n",find(1,n,1,start[b])); //찾기
}
}
//동적할당해제
free(start);
free(end);
for(int i=1; i<=n; i++) {
for(list *p = vec[i].next; p!=NULL; p=p->next) free(p);
}
free(vec);
}
풀이 : 느리게 갱신되는 세그먼트 트리, 오일러 경로 트릭 (ETT)
처음에 그래프가 주어집니다. 구간합, 최소, 최대 등 이전에 풀었던 세그먼트와 다르게 그래프이다보니, 이것을 세그먼트 트리에 바로 적용하기에는 무리가 있습니다.
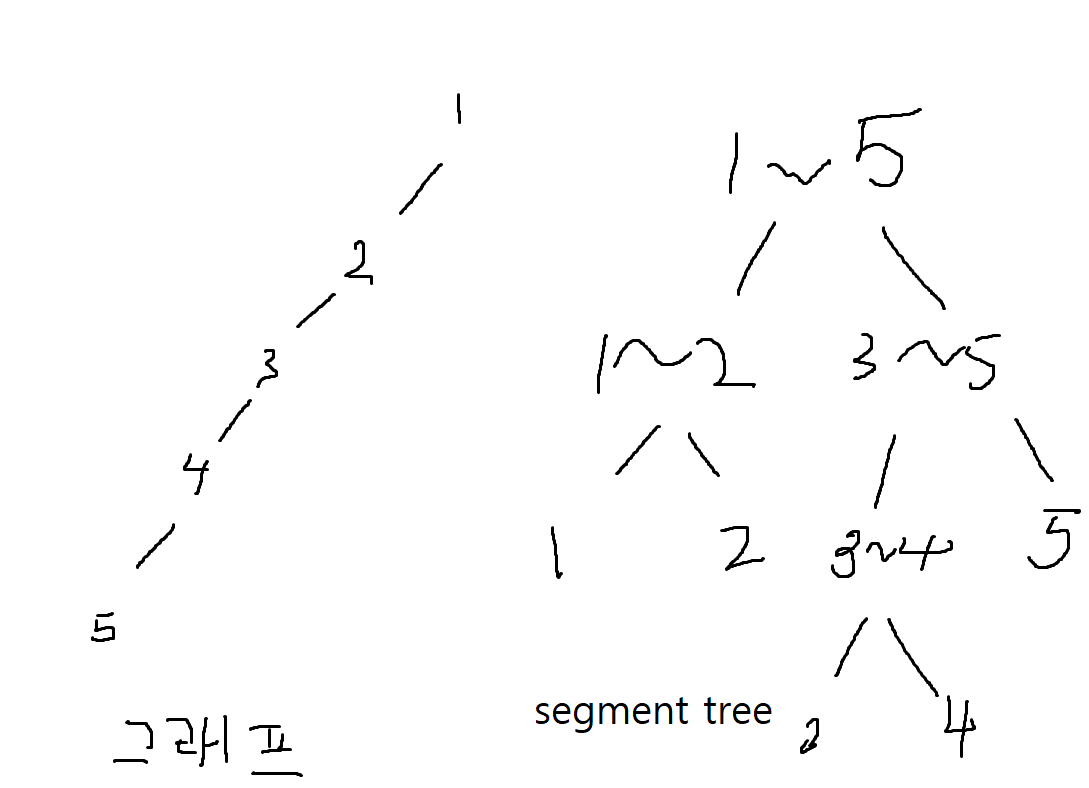
여기서 그래프를 segment tree에서 활용할 수 있도록 만들어주는 테크닉을
오일러 경로 트릭 (ETT) 라고 합니다.
이 트릭은 dfs을 이용하여 각 노드마다 시작번호와 종료번호를 붙여줍니다.
각 노드의 시작번호와 종료번호는, 이 노드를 루트로 하는 하위 노드들의 번호들을 포함한 범위가 됩니다.

ex) 1번 노드 의 시작번호는 1, 종료번호는 5 입니다. 이것은 1을 루트로 하는 노드들이 1,2,3,4,5 (1~5) 라는 의미입니다.
ex) 5번 노드 의 시작번호는 5, 종료번호는 5 입니다. 이것은 5을 루트로 하는 노드들이 5 혼자라는 의미입니다.
이 시작번호와, 종료번호를 이용하여 segment tree에 적용할 수 있습니다.
값을 찾을 때는, 특정 노드를 루트로 하는 모든 노드 들의 값을 알고 싶다면 시작번호~종료번호로 값을 찾으면 되고,
단일 노드의 값을 찾고 싶다면, 찾고 싶은 노드의 시작번호 만을 가지고 값을 찾으면 됩니다.
ex) 3번 노드의 값만 알고 싶다면, 말 그대로 segment tree에서 시작번호만을 가지고 값을 찾으면 됩니다.
추가)
입력을 받아서 노드에 연결되어있는 하위노드를 저장하려면, 배열을 미리 크게 만들어 놓거나, 포인터를 이용하여 임의의 리스트 같은 자료구조를 만들어 놓으면 됩니다.
C++ 로 한다면 STL을 사용하시면 더욱 편리하게 풀 수 있습니다.
펜윅트리로 구현하여 더욱 효율성을 높일 수 있습니다.
'c언어 > BAEKJOON' 카테고리의 다른 글
| c언어 14287번 회사 문화 3 (백준) (0) | 2024.09.05 |
|---|---|
| c언어 2820번 자동차 공장 (백준) (0) | 2024.09.04 |
| c언어 9873번 Cow Baseball (백준) (0) | 2024.09.02 |
| c언어 12895번 화려한 마을 (백준) (0) | 2024.08.29 |
| c언어 2934번 LRH 식물 (백준) (0) | 2024.08.17 |
- Total
- Today
- Yesterday
- 덱
- Krustal
- 그래프
- 그리디
- 정렬
- C++
- DP
- find
- C언어
- union
- 브루트포스
- 세그먼트 트리
- java
- 문자열
- 누적합
- 오프라인 쿼리
- 최소 스패닝 트리
- 기하학
- 백준
- Lazy Propagation
- PASCAL
- Segment Tree
- 구현
- 1835번
- 스택
- DFS
- 누적 합
- BFS
- 1835
- XOR
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
